Πανεπιστημιο Κρητης
Τμημα Επιστημης και Τεχνολογιας Υλικων

Επιστήμη Eπιφανειών - Νανοϋλικών (ΕΤΥ 346)

Τις παρακάτω ασκήσεις θα πρέπει να τις παραδίδετε στη διάρκεια του εξαμήνου. Θα μετρήσουν κατά 10% στον τελικό βαθμό σας, εφόσον όμως τις παραδόσετε όλες (το πολύ να λείπει μια εργασία). Παράδοση μετά την ημερομηνία συνεπάγεται μισό βαθμό. Η λογοκλοπή θα τιμωρείται αυστηρά. Οι ημερομηνίες παράδοσης είναι οι εξής:

• Εργασία 1 (ασκήσεις 1-9): Παράδοση Πέμπτη 13/3/2008.
• Εργασία 2 (ασκήσεις 10-20): Παράδοση Πέμπτη 27/3/2008.
• Εργασία 3 (ασκήσεις 21-26): Παράδοση Πέμπτη 10/4/2008.
• Εργασία 4 (ασκήσεις 27-38): Παράδοση Πέμπτη 15/5/2008.
• Εργασία 5 (ασκήσεις 39-43): Παράδοση Δευτέρα 26/5/2008.

Οι ημερομηνίες παράδοσης και τα περιεχόμενα των εργασιών ενδέχεται να αλλάξουν ελαφρά στη διάρκεια του μαθήματος αν προκύψουν έκτακτες περιστάσεις (πχ καταλήψεις).

Ασκήσεις

Η έννοια της νανοτεχνολογίας

1. Εκτιμήστε πόσα άτομα χρησιμοποιούνται για την αποθήκευση 1 bit πληροφορίας σε ένα (α) cd-rom (β) dvd-rom (γ) usb flash stick. Πάρτε εύλογες εκτιμήσεις για το εμβαδόν, τη χωρητικότητα και όποιες άλλες παραμέτρους χρειαστέιτε.
2. Θεωρώντας ότι χρειάζονται τουλάχιστον 1000 άτομα για να αποθηκευτεί ένα bit πληροφορίας, υπολογίστε τη μέγιστη χωρητικότητα που μπορεί να έχει ένας συμβατικός μεταλλικός σκληρός δίσκος διαμέτρου 3.5 ιντσών.

   Οι βασικές φυσικές ιδιότητες που χαρακτηρίζουν τα νανοϋλικά

3. Υπολογίστε τον αριθμό των επιφανειακών ατόμων καθώς και τον αριθμό των εσωτερικών ατόμων σε ένα κύβο καθαρού σιδήρου ακμής L. Ο σίδηρος φτιάχνει δομή bcc με πλεγματική σταθερά 0.287 nm. Υπολογίστε το λόγο των αριθμών εσωτερικών προς επιφανειακά άτομα σαν συνάρτηση του L. Δώστε τη γραφική του παράσταση.
4. Πρωτόνιο και ηλεκτρόνιο κινούνται σε όμοια καλώδια μήκους L και αμελητέου πάχους, και βρίσκονται το καθένα στην θεμελιώση του κατάσταση. Ποιο από τα δυο θα έχει χαμηλότερη ενέργεια, και ποιος θα είναι ο λόγος των ενεργειών τους;
5. Ηλεκτρόνιο κινείται σε καλώδιο μήκους L και αμελητέου πάχους μεταπίπτει από την δεύτερη διεγερμένη στάθμη στην πρώτη διεγερμένη στάθμη εκπέμποντας ένα φωτόνιο μήκους κύματος 120 nm. Στη συνέχεια μεταπίπτει από την πρώτη διεγερμένη στη θεμελιώδη στάθμη, εκπέμποντας ακόμα ένα φωτόνιο. Υπολογίστε το μήκος κύματός του.
6. Μια προσέγγιση της κίνησης ηλεκτρονίων σε μακρομόρια είναι να θεωρήσουμε ότι κινούνται ανεξάρτητα και με αμελητέες απώσεις Coulomb σε πολύ λεπτό σωλήνα μήκους L, όπου L είναι το μήκος του μορίου. Χρησιμοποιήστε την προσέγγιση αυτή για να υπολογίσετε, σε eV, τις ενέργειες για τις κατειλημένες και τις δυο πρώτες κενές στάθμες των ηλεκτρονίων σε θερμοκρασία T=0, καθώς και την ενέργεια Fermi στο οκτάνιο. Θεωρήστε δυο ηλεκτρόνια σθένους για κάθε άτομο C και ότι οι αποστάσεις μεταξύ ατόμων C είναι 0.15 nm.
7. Χρησιμοιποιείστε τη θεωρία της προηγούμενης άσκησης για να υπολογίσετε το μήκος κύματος της ακτινοβολίας την οποία μπορεί να αποροφήσει το μόριο H₂C=C-CH=...-C=CH₂, το οποίο περιέχει n άτομα άνθρακα με εναλλάξ απλούς και διπλούς δεσμούς. Κάθε άτομο έχει ένα ηλεκτρόνιο σθένους, και οι αποστάσεις μεταξύ ατόμων C είναι 0.15 nm. Βρείτε τις τιμές του n για τις οποίες το μόριο μπορεί να αποροφήσει φωτόνια ορατού φωτός. Σε ποια χρώματα αντιστοιχούν; Τα χρώματα αυτά θα είναι τα χρώματα που θα έχουν οι αντίστοιχες χημικές ουσίες. Γιατί;
8. Θεωρήστε ένα επίπεδο πυκνωτή αποτελούμενο από δυο τετράγωνες μεταλλικές πλάκες πλευράς L, οι οποίες απέχουν L/10 μεταξύ τους. (α) Δείξτε ότι η χωρητικότητα του συστήματος είναι C=10ε₀L (ξεκινήστε από τον ορισμό, C=Q/V). (β) Η πιθανότητα να φορτιστεί ο πυκνωτής με το ελάχιστο δυνατό φορτίο, δηλαδή ένα ηλεκτρόνιο, δίνεται από τον τύπο P=exp(-E/kT), όπου E είναι η ενέργεια που έχει το σύστημα (E=e²/2C), k η σταθερά του Boltzmann και Τ η θερμοκρασία. Υπολογίστε την πιθανότητα αυτή σαν συνάρτηση του L, για θερμοκρασία δωματίου. Τι τιμή έχει σε ένα τυπικό πυκνωτή (L=1 mm) και τι σε ένα νανοσύστημα (L=10 nm);
9. Χρησιμοποιείστε τη θεωρία της προηγούμενης άσκησης για να υπολογίσετε την πιθανότητα να φορτιστεί μια μεταλλική σφαίρα ακτίνας R με φορτίο e σε θερμοκρασία δωματίου. Βρείτε για ποιές τιμές του R η πιθανότητα είναι (α) μεγαλύτερη από 99% και (β) μικρότερη από 1%.

Ατομική δομή στερεών επιφανειών

(Ασκήσεις 10-16) Για τις παρακάτω επιφάνειες:

1. Σχεδιάστε την ατομική δομή τους, δείχνοντας τα άτομα του επιφανειακού επιπέδου καθώς και εκείνα του αμέσως παρακάτω.
2. Βρείτε τα διανύσματα βάσης, σχεδιάστε τα και υπολογίστε τις x- και y-συνιστώσες τους.
3. Υπολογίστε την επιφανειακή συγκέντρωση, n_s.
4. Υπολογίστε την πλήρωση, f.
5. Εκτιμήστε την επιφανειακή τάση (σε J/m²) μετρώντας τον αριθμό των ακόρεστων δεσμών και θεωρώντας ότι κάθε mol ακόρεστων δεσμών στοιχίζει ενέργεια E_coh/z όπου E_coh είναι η ενέργεια συνοχής του στερεού και z ο αριθμός γειτόνων κάθε ατόμου στο εσωτερικό.

10. Fe(100) (O Fe σχηματίζει κρύσταλλο δομής bcc με πλεγματική σταθερά a=0.287 nm και έχει E_coh=414 kJ/mol).
11. Si(110) (To Si σχηματίζει κρύσταλλο δομής διαμαντιού με πλεγματική σταθερά a=0.543 nm και έχει E_coh=450 kJ/mol).
12. Cu(111) (O Cu σχηματίζει κρύσταλλο δομής fcc με πλεγματική σταθερά a=0.361 nm και έχει E_coh=337 kJ/mol).
13. Mg(001) (To Mg σχηματίζει κρύσταλλο δομής hcp με πλεγματικές σταθερές a=0.321 nm και c=0.521 nm και έχει E_coh=147 kJ/mol).
14. Ti(001) (To Ti σχηματίζει κρύσταλλο δομής hcp με πλεγματικές σταθερές a=0.295 nm και c=0.466 nm και έχει E_coh=473 kJ/mol).
15. Na(110) (To Na σχηματίζει κρύσταλλο δομής bcc με πλεγματική σταθερά a=0.429 nm και έχει E_coh=108 kJ/mol).
16. Al(100) (To Al σχηματίζει κρύσταλλο δομής fcc με πλεγματική σταθερά a=0.405 nm και έχει E_coh=330 kJ/mol).
17. Υπολογίστε την πίεση αερίου αργού που απαιτείται ώστε να έχουμε 4.5 10²⁰ συγκρούσεις ανά sec πάνω σε κυκλική επιφάνεια διαμέτρου 2 mm στους 525 Κ.
18. Το Ni σχηματίζει δομή fcc με πλεγματική σταθερά a=0.352 nm. Υπολογίστε πόσα μόρια συγκρούονται με κάθε άτομο της επιφάνειας (111) ανά δευτερόλεπτο μέσα σε ένα δοχείο που περιέχει (α) υδρογόνο ή (β) προπάνιο στους 298 Κ και με την πίεση να είναι (i) 100 Pa ή (ii) 0.10 μTorr.
19. Υπολογίστε το χρόνο που απαιτείται για να σχηματιστεί 1 ML CO στην επιφάνεια Pt(111) στους 200Κ υπό πίεση 1 Torr. Ο Pt έχει δομή fcc με πλεγματική σταθερά a=0.392 nm.
20. To Mo έχει δομή bcc με πλεγματική σταθερά a=0.315 nm. Υδρογόνο προσροφάται στην επιφάνεια Mo(110) με διάσπαση, δηλαδή από κάθε μόριο Η₂ από την αέρια φάση προκύπτουν δυο προσροφημένα άτομα Η. Η πίεση είναι 10^-9 Torr και η θερμοκρασία 300 Κ. Υπολογίστε σε πόσο χρόνο θα έχει προσροφηθεί 0.5 ML.

    Σχήμα των νανοσωματιδίων και επιφανειακές τάσεις

21. Εκτιμήστε την επιφανειακή τάση για τις (100), (110) και (111) του Fe, ο οποίος έχει δομή bcc με a=0.287nm και ενέργεια συνοχής E_c=414 kJ/mol. Τί σχήμα περιμένετε να έχουν τα νανοσωμάτια σιδήρου;
22. Συγκρίνετε την επιφανειακή τάση για την Fe(210) και την Fe(100). Επιβεβαιώστε ότι η επιφανειακή τάση αυξάνεται όσο μεγαλώνουν οι δείκτες Miller. O Fe έχει δομή bcc με a=0.287nm και ενέργεια συνοχής E_c=414 kJ/mol.
23. Εκτιμήστε το σχήμα που θα έχουν οι κρύσταλλοι του κοινού αλατιού, NaCl. Η πλεγματική σταθερά είναι 0.236 nm. Οι ενέργειες συνοχής του στερεού Na και του μορίου Cl₂ είναι 108 kJ/mol και 121 kJ/mol, αντίστοιχα.
24. Θεωρήστε ότι έχουμε ένα νανοσωματίδιο από υλικό το οποίο φτιάχνει κρυσταλλική δομή με κυβική συμμετρία. Γνωρίζουμε ότι η (111) είναι η έδρα με τη χαμηλότερη επιφανειακή τάση. Στην περίπτωση που οι άλλες έδρες (hkl) έχουν επιφανειακές τάσης πολύ υψηλότερες από την (111), το σχήμα ελάχιστης ενέργειας για το νανοσωματίδιο θα είναι κανονικό οκτάεδρο. Δείξαμε στη θεωρία ότι για να μην είναι το σχήμα κανονικό οκτάεδρο, και να εμφανιστούν έδρες τύπου (110), θα πρέπει γ₁₁₀ < √3/√2 γ₁₁₁. Δείξτε ότι:
    1. Για να εμφανιστούν έδρες τύπου (100), θα πρέπει γ₁₀₀ < √3 γ₁₁₁.
    2. Για να εμφανιστούν έδρες τύπου (210), θα πρέπει γ₂₁₀ < 2√3/√5 γ₁₁₁.
    3. Για να εμφανιστούν έδρες τύπου (221), θα πρέπει γ₂₂₁ < 2/√3 γ₁₁₁.
    4. Για να εμφανιστούν έδρες τύπου (211), θα πρέπει γ₂₁₁ < √2 γ₁₁₁.
25. Επαναλάβετε την προηγούμενη άσκηση, θεωρώντας ότι αυτή τη φορά η (100) είναι η επιφάνεια με τη χαμηλότερη επιφανειακή τάση, οπότε το σχήμα ελάχιστης ενέργειας θα είναι κύβος. Βρείτε τις συνθήκες που πρέπει να ικανοποιούν οι επιφανειακές τάσεις τους ώστε να εμφανιστούν έδρες τύπου (110), (111) και (210).
26. Η διεπιφανεική τάση μετριέται συνήθως μέσω της γωνίας επαφής. Υπολογίστε την διεπιφανειακή τάση μεταξύ νερού και των πολυμερών PVC (Poly (vinyl chloride)), PTFE (Poly(tetrafluoroethylene), teflon) και PS (Polystyrene). Βρείτε τις γωνίες επαφής από εδώ και τις επιφανειακές τάσεις από εδώ. Η επιφανειακή τάση του νερού είναι 0.073 J/m².

    Οι παρακάτω τρεις ασκήσεις δεν περιλαμβάνονται στην εργασία 3. Είναι παλιά θέματα, και συζητήθηκαν στο μάθημα της 3/4/08

    • Σε κάποιο υλικό δομής fcc, γνωρίζουμε ότι η επιφάνεια με τη χαμήλότερη επιφανειακή τάση είναι η (100). α) Τι μπορείτε να πείτε για το σχήμα ελάχιστης ενέργειας των νανοσωματιδίων του υλικού αυτού; β) Βρείτε τη συνθήκη που πρέπει να ικανοποιεί η επιφανειακή τάση της (110) ώστε να εμφανίζονται επιφάνειες τύπου (110) στο παραπάνω σχήμα ελάχιστης ενέργειας.
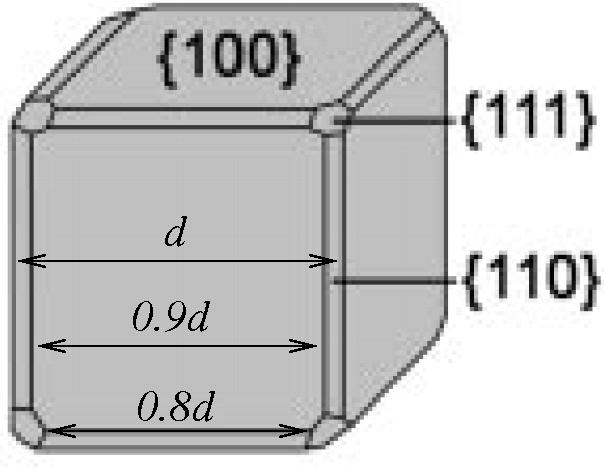    • Σε ένα πείραμα βρέθηκε ότι νανοσωμάτια Ag τα οποία είχαν αφεθεί να φτιάξουν το σχήμα ελάχιστης ενέργειας, είχαν σχήμα όπως αυτό της διπλανής εικόνας. Τι συμπεράσματα μπορείτε να βγάλετε για τις επιφανειακές τάσεις του αργύρου;
    • Ο Β. Φρανγκλίνος έγραφε το 1773: "Αν ρίξουμε μια σταγόνα λάδι [..] πάνω σε οριζόντιο καθρέπτη, η σταγόνα παραμένει στη θέση της, και απλώνεται ελάχιστα. Αν την ρίξουμε σε νερό, απλώνεται αμέσως καταλαμβάνοντας μεγάλη έκταση, και φτιάχνοντας ένα υμένιο τόσο λεπτό ώστε δεν φαίνεται καν. Γίνεται αντιληπτό μόνο από τον ιριδισμό του καθώς ανακλά το φώς.'' Μπορείτε να εξηγήσετε το φαινόμενο? Μπορείτε να εκτιμήσετε πόσο εμβαδόν μπορεί να καταλαμβάνει μια απλωμένη σταγόνα λαδιού πάνω σε απολύτως ήρεμη επιφάνεια νερού; Δίνονται οι επιφανειακές και διεπιφανειακές τάσεις: γ_νερ=0.073 J/m², γ_λαδ=0.036 J/m², γ_καθ=0.047 J/m², γ^int_{λαδ-καθ}=0.030 J/m², γ^int_{λαδ-νερ}=0.023 J/m².

    Προσρόφηση αερίων σε επιφάνειες στερεών

27. Περιγράψτε τις παρακάτω υπερδομές με συμβολισμό Wood. Υπολογίστε κάθε φορά τη συγκέντρωση των προσροφημένων ατόμων ή μορίων.
28. Σας δίνονται εικόνες από πειράματα LEED για τις επιφάνειες Si(100), Si(100) εμπλουτισμένη με C και Si(111). Στις εικόνες που δεν δίνεται η περιοδικότητα της ιδανικής επιφάνειας, Θεωρήστε ότι αυτή αντιστοιχεί στις έντονες κηλίδες. Η σκιά στο κέντρο αντιστοιχεί στο δείγμα και τους βραχίονες στηρίξεώς του. Περιγράψτε την αναδόμηση κάθε επιφάνειας στο συμβολισμό Wood.

    Οι παρακάτω 10 ασκήσεις προέρχονται από το βιβλίο "Φυσικοχημεία" του P. Atkins.

29. 1 ML (monolayer, δηλαδή θ=1.0) αζώτου προσροφάται στην επιφάνεια 1.0 g καταλύτη Fe/Al₂O₃ στους 77 Κ. Θερμαίνουμε τον καταλύτη, και το εκροφώμενο άζωτο καταλαμβάνει 2.86 cm³ σε Κ.Σ. (κανονικές συνθήκες, P=1 atm και T=273 K). Κάθε προσροφημένο μόριο αζώτου καταλαμβάνει επιφάνεια 0.165 nm². Εκτιμήστε το εμβαδόν της επιφάνειας του καταλύτη.
30. Ο όγκος αερίου οξυγόνου που προσροφήθηκε σε 1 g σίλικας στους 273 Κ ήταν 0.284 cm³ όταν η πίεση κατά την προσρόφηση ήταν 142.4 Torr και 1.430 cm³ όταν η πίεση κατά την προσρόφηση ήταν 760 Torr. Οι όγκοι μετρήθηκαν σε Κ.Σ. Υπολογίστε τον όγκο (σε Κ.Σ) οξυγόνου που απαιτείται για να καλυφθεί πλήρως η επιφάνεια στους 273 Κ.
31. Η ενέργεια εκρόφησης CO σε κάποια επιφάνεια μετρήθηκε να είναι -120 kJ/mol. Εξηγείστε αν πρόκειται για φυσιρόφηση ή χημιρόφηση. Εκτιμήστε, για Τ=400 Κ, το χρόνο που περνάει προσροφημένο το CO σε αυτήν την επιφάνεια προτού εκροφηθεί. Υπόδειξη: t=1/k όπου k είναι ο ρυθμός εκρόφησης, k=k₀exp(-E_d/RT). Θεωρήστε ότι k₀=RT/N_Ah, όπου h έιναι η σταθερά του Plank.
32. 'Aτομα οξυγόνου παραμένουν προσροφημένα σε επιφάνεια W για 0.36 sec στους 2548 Κ και για 3.49 sec στους 2362 Κ. Εξηγείστε γιατί ο χρόνος παραμονής αυξάνεται όταν μειωθεί η θερμοκρασία. Υπολογίστε την ενέργεια εκρόφησης και την παράμετρο k₀. (Υπόδειξη: δείτε την προηγούμενη άσκηση).
33. Υπολογίστε πόσο περίπου χρόνο θα παραμείνει προσροφημένο ένα άτομο σε μια επιφάνεια στους 400 Κ, αν η ενέργεια εκρόφησης είναι (α) 15 kJ/mol ή (β) 150 kJ/mol. Θεωρήστε ότι k₀=RT/N_Ah. Επαναλάβετε την άσκηση για Τ=1000 Κ.
34. Προσρόφηση κάποιου αερίου σε κάποια επιφάνεια περιγράφεται από τον τύπο του Langmuir με Κ=0.85 (kPa)^-1. Υπολογίστε την πίεση για την οποία η συγκέντρωση θ είναι (α) 0.15 και (β) 0.95.
35. Κάποιο στερεό προσροφά 0.44 mg CO σε πίεση 36.0 kPa και θερμοκρασία 300 Κ, ενώ σε πίεση 4.0 kPa και θερμοκρασία 300 Κ προσροφά 0.21 mg. Γνωρίζουμε ότι η προσρόφηση περιγράφεται από τον τύπο του Langmuir. Υπολογίστε την επιφανειακή συγκέντρωση, θ, για τις δυο παραπάνω τιμές της πίεσης.
36. Υποθέστε ότι η προσρόφηση του όζοντος σε κάποια επιφάνεια περιγράφεται από τη θεωρία του Langmuir. Εξηγείστε τι πειράματα θα εκτελούσατε για να εξακριβώσετε αν η προσρόφηση γίνεται (α) μοριακά ή (β) με διάσπαση σε Ο+Ο₂ ή (γ) με διάσπαση σε Ο+Ο+Ο.
37. Εκτελούμε πείραμα προσρόφησης αζώτου σε κάρβουνο. Στους 190 Κ και υπό πίεση 490 kPa, απαιτούνται 0.921 cm³ αζώτου (μετρημένα σε Κ.Σ) ανά γραμμάριο κάρβουνου. Στους 250 Κ, για να επιτύχουμε προσρόφηση ίσης ποσότητας αζώτου απαιτείται πίεση 3.2 MPa. Υπολογίστε την ενθαλπία προσρόφησης του αζώτου στο κάρβουνο.
38. Τα παρακάτω δεδομένα αφορούν χημιρόφηση υδρογόνου σε ρινίσματα χαλκού στους 298 Κ. P είναι η πίεση του αερίου υδρογόνου, και V o όγκος του προσροφημένου αερίου, μετρημένος σε Κ.Σ. Επιβεβαιώστε ότι περιγράφονται από τον τύπο του Langmuir. Υπολογίστε τη σταθερά K και τον όγκο προσροφημένου υδρογόνου ο οποίος αντιστοιχεί σε πλήρη κάλυψη.

    P (Torr)	0.19	0.97	1.9	4.1	7.5	12.
    V (cm3)	0.04	0.16	0.22	0.32	0.41	0.47

    Κατάλυση

39. Στις κυψέλες καυσίμου χρησιμοποιείται καταλύτης Pt στον οποίο το υδρογόνο προσροφάται με διάσπαση, και εν συνεχεία τα άτομα υδρογόνου χρησιμοποιούνται για την παραγωγή ενέργειας. Το αέριο υδρογόνο όμως περιέχει και ίχνη CO, το οποίο επίσης προσροφάται στην επιφάνεια. Καθώς μάλιστα έχει μεγαλύτερη ενέργεια εκρόφησης (E_d^CO=100 kJ/mol ενώ E_d^Η=80 kJ/mol), καταλαμβάνει τις περισότερες θέσεις στην επιφάνεια, μη αφήνοντας χώρο για το υδρογόνο. Υπολογίστε τις συγκεντρώσεις θ_H, θ_CO και θ_* για P=1 bar και θερμοκρασία 80^oC, όταν η περιεκτικότητα του υδρογόνου σε CO είναι (α) 1 ppm ή (β) 10 ppm ή (γ) 100 ppm. Δίνεται ότι η επιφάνεια του καταλύτη είναι Pt(111) και ο Pt έχει δομή fcc με α=0.392 nm, και οι σταθερές της ταχύτητας αντιδράσεων (ν=10¹³ sec^-1):

    H2+2*↔2H*	k1+=2/ns√(2πmH2kBT)	k1-=v exp(-EdΗ/RT)
    CO+*↔CO*	k2+=1/ns√(2πmCOkBT)	k2-=v exp(-EdCO/RT)

40. Το άεριο άζωτο προσροφάται σε καταλύτη Ru, και εν συνεχεία διασπάται σε άτομα αζώτου. Οι αντιδράσεις και οι τύποι που δίνουν τις σταθερές ταχύτητας αντίδρασης είναι:

    N2+*↔N2*	k1+=P/ns√(2πmN2kBT)	k1-=v1 exp(-Ed/RT)
    N2*+*↔2N*	k2+=v2 exp(-Ea/RT)	k2-=v2' exp(-Ea'/RT)

    (α) Δικαιολογήστε τη μορφή που έχουν οι τύποι για τις σταθερές ταχύτητας. (β) Υπολογίστε τη συγκέντρωση ατόμων αζώτου και κενών θέσεων σαν συνάρτηση της πίεσης του αζώτου και της θερμοκρασίας. Θεωρήστε ότι έχουμε θερμοδυναμική ισορροπία. Πάρτε v₁=v₂=v₂'=RT/N_Ah, όπου h έιναι η σταθερά του Plank. Για να βρείτε το n_s, θεωρήστε την Ru(001) και ότι το Ru έχει δομή hcp με α=0.271nm. Πάρτε τις ενέργειες που μπαίνουν στους τύπους από το θεωρητικό υπολογισμό της εικόνας. Θεωρήστε δυο περιπτώσεις: Πρώτα προσρόφηση σε άτομα Ru που βρίσκονται σε επίπεδο (terrace) και μετά προσρόφηση σε άτομα Ru που βρίσκονται σε σκαλοπάτι (step).
41. Το προηγούμενο πρόβλημα μπορεί να λυθεί και χωρίς να υποθέσουμε χημική ισορροπία. Μπορούμε δηλαδή να εξάγουμε πώς εξαρτώνται οι συγκεντρώσεις από το χρόνο, και όχι απλά τις αυμπτωτικές τιμές τους μετά από άπειρο χρόνο.
    (α) Δείξτε πρώτα ότι απαιτείται λύση συστήματος 4 διαφορικών εξισώσεων με 4 άγνωστες συναρτήσεις:
    dp_N2/dt=-k₁⁺ p_N2θ_* + k₁^- θ_N2
    dθ_*/dt = -k₁⁺ p_N2θ_* + k₁^- θ_N2 - k₂⁺ θ_N2θ_* + k₂^- θ_N²
    dθ_N2/dt = k₁⁺ p_N2θ_* - k₁^- θ_N2 - k₂⁺ θ_N2θ_* + k₂^- θ_N²
    dθ_N/dt = -2 k₂^- θ_N² + 2 k₂⁺ θ_N2 θ_*
    Οι αρχικές συθήκες είναι ότι για t=0 έχουμε p_N2=1, θ_*=1 και θ_N2=θ_N=0.
    (β) Δείξτε ότι στη χημική ισορροπία, όπου οι συγκεντρώσεις δεν εξαρτώνται από το χρόνο, οι εξισώσεις δίνουν τα αποτελέσματα της προηγούμενης άσκησης.
    (γ) Δείξτε ότι σε κάθε χρονική στιγμή θ_*+θ_N2+θ_N=1.
    (δ) Μας ενδιαφέρουν πιέσεις της τάξεως των 100 bar, και θερμοκρασίες μερικών εκατοναδων βαθμών Κελσίου. Δικαιολογήστε, με βάση τους τύπους της προηγούμενης άσκησης και το σχήμα ότι σε αυτές τις συνθήκες η k₁⁺ είναι κατά πολύ μεγαλύτερη από τις άλλες, και ότι οι k₂⁺ και k₂^- θα είναι περίπου ίσες.
    (ε) Ακόμα και με την προσέγγιση αυτή, όμως, προκύπτει μή γραμμικό σύστημα το οποίο δεν λύνεται ακριβώς. Πάντως λύνεται πολύ έυκολα αριθμητικά. Αν είστε δυνατοί στις διαφορικές εξισώσεις και στην υπολογιστική επιστήμη υλικών, δοκιμάστε το!
42. Ο λευκόχρυσος χρησιμοποιείται ως καταλύτης για την καύση του υδρογόνου (στις αρχές του 19ου αιώνα φτιάχτηκαν οι πρώτοι αναπτήρες οι οποίοι λειτουργόυσαν με αυτή την αρχή!). Η αντίδραση ξεκινάει με την προσρόφηση του οξυγόνου και του υδρογόνου στην επιφάνεια. Και οι δυο προσροφήσεις γίνονται με απευθείας διάσπαση. Στη συνέχεια, τα O* και H* ενώνονται για να φτιάξουν υδροξύλιο, το οποίο εν συνεχεία γίνεται νερό με προσθήκη ενός ακόμα υδρογόνου.
    (α) Δικαιολογήστε ότι η ανιδραση O*+H*↔OH*+* είναι πολύ πιο αργή από τις άλλες και επομένως θα καθορίζει την ταχύτητα (RDS).
    (γ) Δείξτε ότι η ταχύτητα της αντίδρασης είναι ανάλογη του
    (P_H2P_O2)^0.5θ_*².
    (δ) Υπολογίστε το θ_* θεωρώντας ότι οι το οξυγόνο έχει πολύ μεγαλύτερο ποσοστό επικάλυψης από ότι το υδρογόνο, ενώ το νερό έχει αμελητέο θ.
    (ε) Θεωρήστε ότι P_H2O=0.1P_H2, και ότι P_H2+P_O2=1. Βρείτε την τιμή της πίεσης του υδρογόνου στην οποία η ταχύτητα της αντίδρασης γίνεται μέγιστη.
43. Η σύνθεση της αμμωνίας με τη μέθοδο Haber-Bosch έχει τα ακόλουθα ενδιάμεσα στάδια (δίνονται και οι σχετικές εξισώσεις):

    N2+*↔N2*	θN2=Κ1PN2θ*	(1)
    N2*+*↔2N* (RDS)	r=k θN2θ* - (k/K2) θN2	(2)
    N*+H*↔NH*+*	θN=θNHθ*/(K3θH)	(3)
    NH*+H*↔NH2*+*	θNH=θNH2θ*/(K4θH)	(4)
    NH2*+H*↔NH3*+*	θNH2=θNH3θ*/(K5θH)	(5)
    NH3*↔NH3+*	θNH3=(1/K6)PNH3θ*	(6)
    H2+2*↔2H*	θH=√(Κ7 PH2) θ*	(7)
    Αριθμοί επιφανειακών θέσεων:	θN2+θN+θNH+θNH2+θNH3+θH+θ*=1	(8)

    Εμπειρικά, χρησιμοποιείται ο τύπος

    r=a (K_GP_N2-P_NH3²/P_H2³)/ (1+γP_NH3/P_H2^w)².

    Βρείτε τη σταθερά w. Πώς σχετίζονται οι άλλες σταθερές στον εμπειρικό τύπο με τις σταθερές των παραπάνω επιμέρους αντιδράσεων;

Αρχική

Ημερολόγιο

Βιβλία/σύνδεσμοι

Ασκήσεις

Βαθμολογίες

---

Τελευταία τροποποίηση την 12/5/2008 από τον Γιάννη Ρεμεδιάκη.